La boite à sucre une boite pleine où il y a encore de la place
La boite à sucre ou pour d'autre la boite magique, le rangement de coffre, ou encore red stone est une application logique de propriétés connues et largement utilisées dans les casse-tête et puzzles!
D'ailleurs je considère que les maths ne sont que le langage pour décrire ou comprendre le monde qui nous entoure.
Voici un exemple qui utilise simultanément plusieurs propriétés:
1) 27= 3*3*3 et 28= 2*2*7
2) la suite de Fibonacci; 1, 2, 3, 5, 8; 13....et ses propriétés.
3) une approximation du type 3 longueurs de sucre unitaire est "presque" égal à 7 fois l'épaisseur unitaire.
Muni de ce bagage l'explication de la solution de la boite à sucre devient facile et évidente.
En partant d'une brique en forme de sucre aux dimensions particulières, on va voir pourquoi plus loin...
exemple, 14*22*33 en mm, on peut construire deux parallélépipèdes:
Un de 27 sucres en 3*3*3 au total donc, de 3* 14= 42 de haut, 3*22 = 66 de large, 3*33 = 99 de long
et un de 28 sucres en 2*2*7 au total donc, de 2*22 = 44 de haut, 2*33 = 66 de large, 7*14 = 98 de long
ces deux parallélépipèdes ont des dimensions "presque" identiques et on a juste changé l'orientation de l'empilement des sucres et le nombre de sucres.
Si les cotes internes de la boite font 1 mm de plus que chaque cote la plus grande soit: 44+1= 45 de haut, 66+1= 67 de large, 99+1= 100 de long elle peut contenir ces deux volumes de 27 ou 28 sucres avec un jeu maximal de 2mm peu visible surtout sur la hauteur (vue sans le couvercle) et un seul mm sur la largeur et la longueur. On a donc les cotes internes de la construction de la boite dont l'épaisseur est elle, quelconque...
Il reste à décomposer ces deux parallélépipèdes en un ensemble de plusieurs pièces (8 dans notre exemple) et composées d'un multiple du sucre unitaire qui constitue la 9° pièce:
U le sucre supplémentaire identique à A et donc aussi Unitaire mais de couleur différente
A le sucre identique à l'unitaire épaisseur a=14 mm et 22*33
B une pièce de 2*a, bout à bout " " et 22*66
C une pièce de 2*a, cote à cote " " et 33*44
D une pièce de 4*a, en carré " " et 44*66
E une pièce de 2*a, superposés épaisseur 2a= 28 mm et 22*33
F une pièce de 4*a, ou 2*B " " et 22*66
G une pièce de 4*a, ou 2*C " " et 33*44
H une pièce de 8*a, ou 2*D " " et 44*66
On a donc les cotes de construction de toutes les pièces
La solution et la manipulation de l'ensemble devient alors simple et évidente!
On peut alors l'accompagner d'un discours pour troubler l'assistance.
exemple:
"C'est un banquier dont le coffre est plein de lingots de différentes tailles! Il reçoit un client qui veut lui confier un lingot d'or pour une nuit. Le banquier vide le coffre et arrange les lingots... et pour finir il rentre tout et ferme le coffre."
une la vidéo d'un autre.
Les relations entre les cotes et les calculs des cotes des pièces en fonction de a la plus petite cote, l'épaisseur du sucre unitaire sont comme suit:
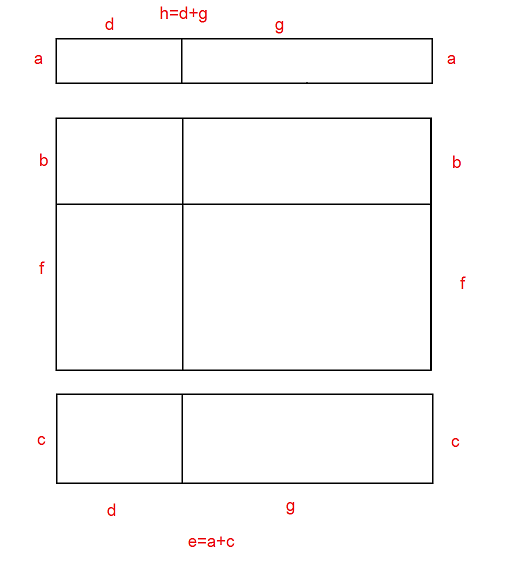
avec c=2a, e=a+c=3a, d≈7a/3, g=2d, b=g/3, f=2b, h=3d
donc en partant de a=14 on calcule d=14*7/3= 32.66666 arrondi à 33 puis g=66 puis b=66/3=22, puis f=66, h=3*33=99
On sait déjà que e= a+c et h=d+g
On a maintenant une méthode pour construire un jeu de pièces à partir de n'importe quelle cote "a" de départ!
Ce qui permet des variantes en partant de la plus petite des dimensions, la hauteur du sucre unitaire "a".
Il faut remarquer que le volume de la boite de notre exemple est de 45*67*100 soit 301500 mm3
que le volume du paquet avec le U compris donc 28 sucres est de 98*66*44 soit 284592 mm3
et que la différence est de 16908 qui est supérieur au volume d'un troisième sucre de 14*22*33= 10164 mm3 !
Mais il faudra le réduire en poudre pour l'introduire dans l'espace disponible, car il n'existe pas d'arrangement pour 10 pièces entières...
Pour ceux qui n'ont pas le temps de le construire achetez le chez Logica.
Qui a aussi une vidéo où il le qualifie de difficile et compliqué et je ne suis donc pas "d'accord" puisque je viens de démontrer le contraire...
Mais il n'est pas le seul les ricains aussi font des vidéos complexes, en plus ils le vendent 99$ en gros 5 fois plus cher! de l'arnaque pure surtout quand on rajoute les frais d'expédition.
Pour aller plus loin il y a déjà dans mes blogs des ressemblances avec:
- 27= 3*3*3 et 28= 2*2*7 une propriété qui fonctionne comme dans le plus ou moins avec
- 1, 2, 3, 5, 8; 13... la suite de Fibonacci.
Ce qui permet de construire le nombre d'or et l’angle d’or avec ses propriétés comme le découpage de Lewis Carol qui lui concerne le plan.
- Ou l'approximation 7a≈3d ressemble à la construction de la musique en utilisant 12 octaves≈7quintes
- les problèmes de rangements de parallélépipèdes voir le cube de Dean Hoffmann
On comprend mieux les astuces mathématiques cachées derrière les propriétés de ces casse-tête, la musique, le nombre d'or, et autres...
Une vidéo du même casse-tête mais sans couvercle, sans discours, sans les cotes, sans les explications des maths pour manipuler sans avoir à mémoriser les emplacements:
La version de cette vidéo est inspirée de la boite bondée attribuée à T.H. O'Beirne décrite dans le livre 1000 casse-tête du monde entier page 81.
Elle n'utilise pas exactement les mêmes ordonnancements et cotes. la description dans ce livre comporte un erreur sur les cotes de la boite facile à détecter et corriger. Le livre 1000 casse-tête du monde entier n'en reste pas moins une mine pour les amateurs de cette discipline.
Un internaute a utilisé l'article pour mettre les équations en langage Python sur le site de l’air du bois.
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 197 autres membres