Puzzles & casse-tête en bois gratuits à fabriquer, construire soi-même

Il s'agit d'un rangement classique de 27 parallélépipèdes tous identiques dans un cube. Une véritable merveille de simplicité puisque les parallélépipèdes vont se placer dans un rangement du cube de type 3*3*3, mais un casse-tête redoutable dont la solution est difficile à trouver, car il est particulièrement ardu de mémoriser une orientation et en plus les faces sont très semblables.

Les côtes des parallélépipèdes sont A, B, C avec  A<B<C et 3A>B+C ou ce qui est équivalent A>(A+B+C)/4. Ce qui se traduit par le plus petit coté d'un parallélépipède est plus grand que le quart du coté du cube.

le coté du cube qui doit les contenir est alors égal à A+B+C.

Cette possibilité est  assurée car l'inégalité  27A*B*C<(A+B+C)3 pour tout triplet de nombres positifs A<B<C qui vérifient A>(A+B+C)/4 a été démontrée par Dean Hoffman en 1978 à Miami lors d'une conférence.

Ce qui se traduit par " le volume du cube est plus grand que le volume total des parallélépipèdes".

On peut prendre par exemple les côtes suivantes A=40 B=45 C=50, le coté du cube est alors de: 40+45+50=135.

Pour le construire on part d'un carrelet raboté de 50*45mm. Il reste alors à découper en tranche de 40mm les 27 parallélépipèdes.

La principale difficulté reste de repérer les orientations et de  distinguer les différents cotés lors des essais. La solution la plus simple qui permet aussi de noter la position d'une solution, consiste à colorier chaque côte d'une même dimension (parallèlement à cette côte) par une couleur différente (par exemple avec des stabilos surligneurs fluorescents ).

il est alors facile de vérifier d'un coup d'œil qu'une rangée ou une colonne comporte les trois couleurs

pour augmenter le contraste des lignes fluo le fond a été blanchi avec une teinture bois.

exemple A rouge, B vert, C jaune comme dans la photo suivante:

Les 27 morceaux:

pour la présentation coller quatre façades de plastique transparent de 135x136+e (135+1mm pour le jeu et d'épaisseur du pléxy) comme sur la photo ci-dessous . On obtient un cadre sans fond:

 démonstration rien ne dépasse:

Ce casse-tête est vendu par philos et il y est dit que la solution est unique. Ce qui est parfaitement faux puisque  Bill Cutler indique qu'il en existe 21 différentes dans un article. cet article donne d'ailleurs de nombreux autres problèmes de rangements mais pas les solutions.

Une solution en couleurs

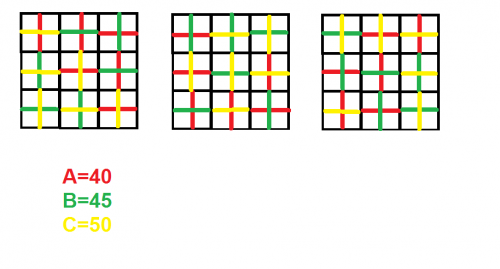
Les 21 solutions malheureusement en anglais mais les dessins parlent d'eux-même:

(un grand merci à Jean Poldeux qui me les a communiqués sur le forum de Chantal)

https://alexey.im/papers/hoffman-puzzle-for-conway.pdf