Le plus (ou moins et beaucoup plus)
Les variantes de ce casse tête sont inspirées de l'une des inventions d'un des meilleurs inventeurs Français
« Patrick Farvacque » son site "défi jeux" à disparu depuis son décès.
Je l'ai rencontré au salon des jeux mathématiques ou il présentait sa collection absolument époustouflante de création et d'inventivité.
Le plus ou moins est typiquement un casse-tête qui fait dire immédiatement « ce n'est pas possible » et comme d'habitude ça l'est quand même.
On vous donne un ensemble de 8 pièces qui tiennent assemblées dans une enveloppe plastique parallélépipédique, sans vide intérieur et on vous demande d'insérer le PLUS dans l'assemblage de telle manière que l'ensemble remplisse encore l'enveloppe plastique initiale sans déborder ni allonger ou distendre l'enveloppe.
l'ensemble dans l'enveloppe (sauf le + )
Les 9 pièces


La pièce en plus est:
- une croix que l'on nomme le Plus le x des pentacubes
L'ensemble est donc composé d'une famille de 9 pièces de 5 cubes (un cousin des pentacubes) qui sont tous les assemblages différents dans l'espace par rotation ou retournement de deux pièces:
une de deux cubes accolés
une de trois cubes alignés
Et une croix qui est l'assemblage de 3 cubes alignés et d'un cube de chaque coté du milieu (ça reste une pièce de 5 cubes) elle ressemble à un + et ça tombe bien.
Voir la photo des pièces 1 à 9.
Au départ on a un parallélépipède de 2*4*5 soit 40 cubes composé des 8 pièces insérées dans une enveloppe en plastique de 12*5 carrés, fermée par un ruban adhésif, et le plus (ou + ).
Le périmètre de l'enveloppe est de 12 soit (2+4)*2 et sa hauteur est de 5 carrés.
On peut y insérer une pièce de plus le X (ou +) mais comment???
Sachez que le principe m'a demandé trois minutes mais la solution de l'arrangement pour y glisser le X m'a demandé une dizaine d'heures sur trois soirées pour le plus en fait le temps de comprendre et pratiquer ce groupe particulier.
Construisez le et cherchez!!
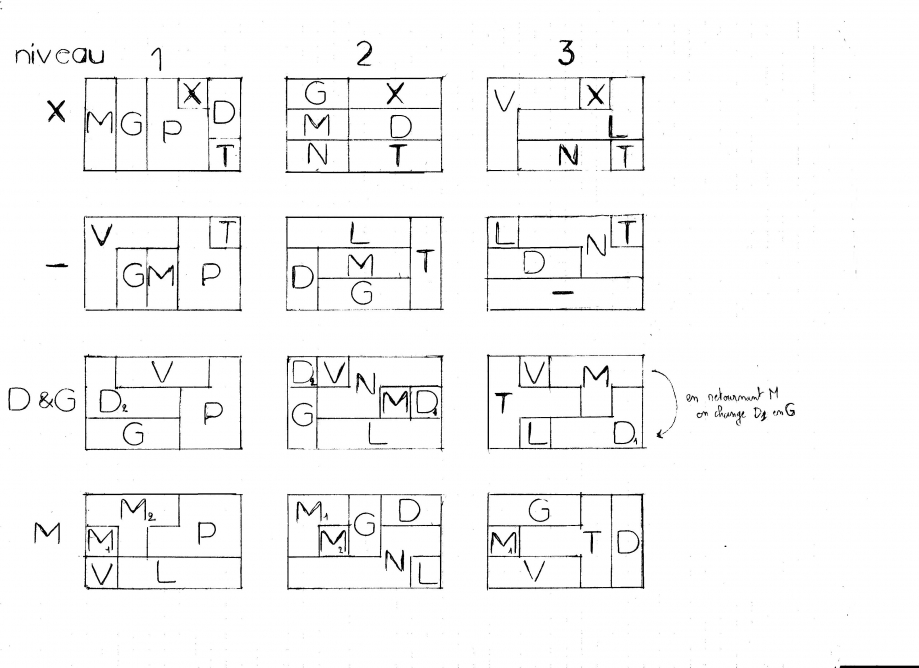
La solution:
La solution:
Ne regardez pas tout de suite !! faites un effort!
La solution passe par une propriété simple:
Au départ on a un volume de 2*4 sur une hauteur de 5 soit 40 cubes unitaires donc 8 fois cinq éléments de 5 cubes.
On doit rentrer dans l'enveloppe un élément de plus soit 45 cubes unitaires.
Comme on ne peut changer la hauteur il faut jouer sur le périmètre, Initialement 2*4 soit 12 de périmètre soit 8 cubes en surface.
Le périmètre d'un carré de 3 donne également un périmètre de (3+3)*2 soit 12
et 3*3=9 de surface soit 8+1.
Donc en faisant un volume de 3*3*5 de haut on peut rentrer 45 cubes dans l'enveloppe, donc il est possible d'insérer une pièce de plus. Mais comment là est la question?
Une fois trouvée la solution on peut étendre le problème aux autres pentacubes.
Une fois trouvée la solution on peut étendre le problème aux autres pentacubes.
J'ai tout d'abord pensé au moins, le I des pentaminos et trouvé une solution en une heure environ.
Puis je me suis posé la question pour les autre pentaminos plats comme le L, N, P T, V, les pièces respectives N°6, 9, 4, 8, 7.
et aux pièces spécifiques (Les Gauche N°1, Droite N°2 et Milieu N°3) d'abord mais aussi les autres pentacubes non plan alpha beta, gama, delta, ainsi de suite...
Dénominations et forme de l'ensemble des pièces:
Les dénominations pour l'article des pièces N°
1 bras droit
2 bras gauche
3 milieu
4 P
5 + ou plus
6 L
7 V
8 T
9 P
10 - ou moins ou I
11Y
12 F
13 U
14 W
15 Z
alpha
beta
gama
delta
Et les solutions que j'ai trouvées tout seul pour le + et le - mais on peut étendre le problème à l'ensemble des pièces du jeu et même des pentacubes, ce qui n'est pas indiqué dans son livret joint au jeu.
Puis j'ai trouvé d'abord celles pour le Z et le U
Puis en cherchant pour les autres, j'ai une solution (voir plusieurs) pour les T, P, L, W,V, Y,F, N, droite, gauche et milieu donc les pentacubes plans.
Puis de plus en plus aussi pour tous les autres pentacubes non plans une véritable jubilation.
Finalement il en existe pour tous les 29 pentacubes même non plans voir les pentacubes.
Ce groupe de 8 pièces composé d'un mélange de pentacubes plans et non plans possède des propriétés bien plus complexes que celle utilisée par Patrick Farvacques pour le seul X ou plus!
La vidéo d'une variation de problèmes à 35 pentacubes comprenant les pentacubes non plans pour faire un parallélépipède de 5*5*7
Les autres articles en liens sur le sujet des pentacubes:
Retour aux articles de la catégorie casse-tête à construire ou connaître -
⨯
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 197 autres membres