Puzzles & casse-tête en bois gratuits à fabriquer, construire soi-même

Les pentaminos sont des assemblages de cinq cubes identiques et unitaires

il en existe de trois types:

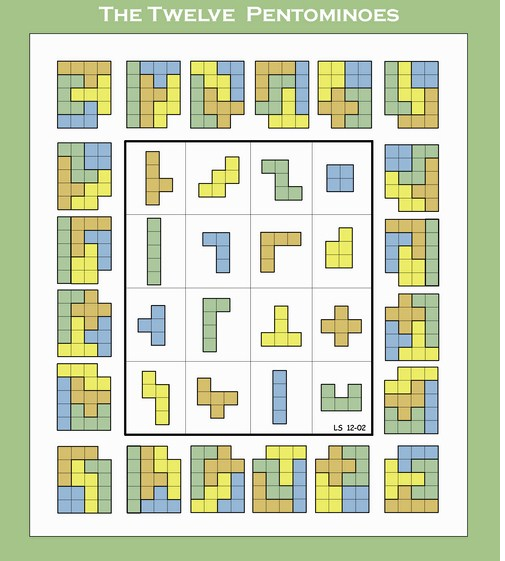
- les pentaminos plats et qui sont leur propre symétrique dans une glace quelques fois par retournement, il y en a 12

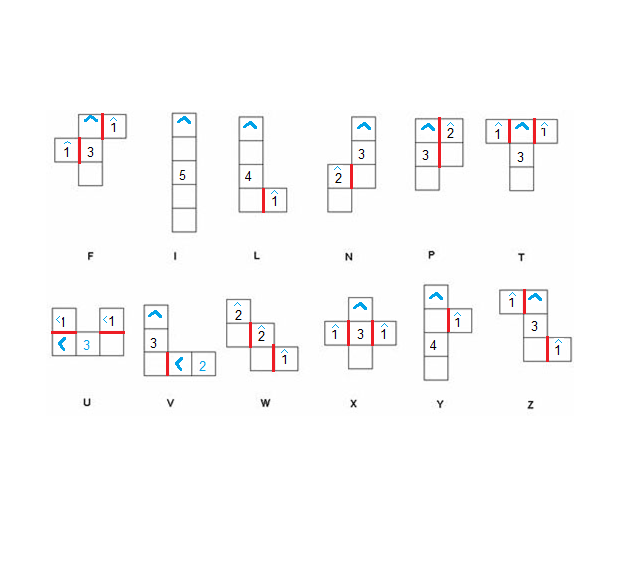
- les pentominos non plats qui ont un symétrique gauche/droite, c'est à dire qui ont reflet dans une glace qui ne sont pas superposables comme une main gauche et une main droite. il y en a 6 gauches et 6 droites donc 6 types de paires qui se déclinent en un droite et un gauche.

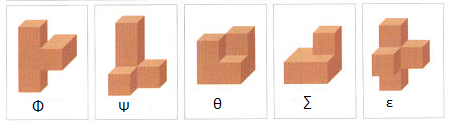
- les pentominos non plats qui sont leur propre symétrique dans une glace il y en a 5

Les 12 plats repérés par leur ressemblance avec une lettre de l'alphabet latin ce mode de repérage est assez bien partagé car logique:

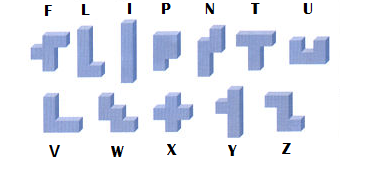
Les 12 pentominos non plats et non symétriques repérés par 6 types de 1 à 6 avec une version g gauche et d droite ce mode de repérage n'est pas universellement admis il existe d'autres méthodes.

Les 5 pentominos non plats et symétriques d'eux même! Φ Ψ θ ∑ ε repérés par des lettres grecs ou symboles physiques ou mathématiques c'est un repérage qui m'est personnel mais il fallait bien trouver une appellation.

Fabrication des douze pentacubes plats (ou pentaminos)

avec un carrelet (morceau de bois carré par ex 20*20mm raboté, parfaitement d'équerre et en bois dur type chêne) de longueur minimum 1345 mm marquer le coté du dessus avec un V et débiter selon le tableau ci-dessous. Coller selon croquis à la colle vinylique en veillant à ne pas glisser au serrage (en enfonçant une ou deux petites aiguilles coupées à quelques millimètres par exemple) et en gardant toujours la même face sur le dessus et le sens pour conserver les éventuels faux équerrages.
Seul le U demande à être collé avec un espacement d'un carré plus un peu de jeu pour ne pas serrer sur les cotés des autres pentominos (ou faire le jeu en ponçant les faces intérieurs après collage).
Il ne reste plus qu'à poncer légèrement et teinter selon ses goûts.

Cubes 1*1*1= 17 (dont 4 pour l'échiquier)

Barres 1*1*2= 4

Barres 1*1*3= 8

Barres 1*1*5= 2

Barres 1*1*5= 1
TOTAL        =64*(le coté+trait de scie)
exemple avec trait de scie=1 mm
Total=64*21=1344 mm
En rouge les collages à la colle vinylique
Faire une boite de 8*8 carrés + un jeu raisonnable (1mm) environ pour ranger l'ensemble.

 

les douze pentacubes peuvent être fait soit:

- dans une seule et même essence de bois qui peut être uniforme et non teintée

- dans une seule et même essence de bois qui sera teintée de couleur différente pour chaque pièce

- dans des essences différentes de bois pour chaque pièce, etc...

 

Pour éviter des déformations non uniformes je favorise les solutions avec une même essence de bois

 

 

 

La méthode pour construire les autres pentacubes non plats est de la même mouture mais on utilisera des cales pour avoir des décalages exacts comme dans l'article pyramide de cube.

 

 

le banc de collage avec les cales

 

 

 

les empillements avec les cubes sur les cales

 

 

 

Les problèmes