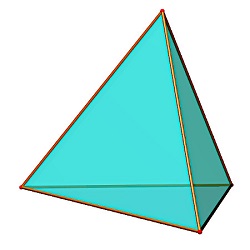
Le tétraèdre
Le tétraèdre est un volume obtenu en assemblant 4 triangles isocèles. Cela ressemble donc à une pyramide à base triangulaire et donc non carré contrairement à celles des égyptiens qui ont une base carrée...
le tétraèdre fait partie des solides de platon.
Il existe un grand classique des casse-tête qui est constitué de 2 pièces identiques pouvant le reconstituer, donc un tétraèdre coupé en deux.
Il est tellement simple qu'on peut le croire sans intérêt, et pourtant chaque fois que je le présente à un public non averti il pose des problèmes à ceux qui sans le connaitre, pensent le résoudre facilement.
Pourquoi??
Le tétraèdre sur youtube
le tétraèdre sur dailymotion
Le temps maximum observé pour trouver la solution est de 20mn ce qui démontre la force de l'habitude et le temps moyen tourne autour de 2 à 3mn ce qui est très étonnant en regard de sa simplicité.
Du coup pour agacer encore plus le public je l'ai baptisé "le casse-tête pour blonde de quatre ans" en rajoutant que: " moins de deux pièces c'est une seule et une seule pièce, ce n'est plus un puzzle!"
Bien sûr certains vont le trouver en moins de dix secondes mais la grande majorité des gents commence par douter de la possibilité qu'une solution existe et ne trouve la solution qu'en plusieurs minutes qui leur semblent interminables et après des tentatives qui apparaissent comme de plus en plus vaines.
Pourquoi un casse-tête aussi trivial pose tant de difficultés à la plus-part des gents?
C'est parce que notre cerveau est habitué à rechercher des symétries surtout lorsque deux pièces absolument identiques doivent s'assembler. Cette habitude contrarie la réflexion pour la recherche de la solution qui, justement, n'est pas symétrique. L'énervement et la contrariété envahissent rapidement le cobaye qui sent le ridicule monter en lui, et la honte de ne pas trouver alors qu'un enfant dont le cerveau est moins (dé)formé arrive généralement plus rapidement à découvrir cette solution. Le cobaye qui cherche la solution passe par la solution sans remarquer qu'il a trouvé parce que son cerveau lui indique que ce n'est satisfaisant car non symétrique...
Un conseil ne jamais donner la solution car cela retire automatiquement la joie de trouver par soi-même alors que chacun finira toujours par y arriver.
On peut donner de l'aide justement en indiquant que la solution n'est pas symétrique mais pas la solution. Une fois la curiosité excitée et le contact engagé il sera facile d'aborder des casse-tête de plus en plus élaborés. C'est donc quasiment toujours le premier casse-tête que je présente en public avec la certitude d'étonner et de surprendre, tout en faisant comprendre que notre propre cerveau peut nous freiner dans notre réflexion.
Les deux pièces identiques et la solution pourtant triviale:

En fait les arrêtes opposées sont perpendiculaires et non pas parallèles ce qui contrarie notre besoin de symétrie.
La géométrie du tétraèdre est à l'avenant car il est certes l'assemblage régulier de quatre triangles équilatéraux (donc cotés égaux et angles de 60° pour chaque face, mais pas sur le volume entre faces contigües).
Donc pour sa fabrication avec une scie sur table, démarrer la fabrication en coupant avec des angles de 60° ne permettra pas d'obtenir un tétraèdre.
Il faut remarquer d'abord que chaque morceau possède une face carré dont le coté est égal à la moitié du coté des triangles équilatéraux. Bizarrement un tétraèdre composé de quatre triangles cache trois carrés qui coupent les quatre faces exactement en leurs milieux.
Les arrêtes reliant les sommets sont perpendiculaires deux à deux et non parallèles. Mais on ne peut pas partir d'un tétraèdre que l'on coupe en deux car l'épaisseur du trait de scie modifie les côtes en raison de l'épaisseur de la lame et il est très difficile de déterminer les angles et calage de coupe pour tomber juste même avec une lame mince.
Si on prend cette face carré comme face de référence posée sur la table de la scie, le profil triangulaire dans lequel est découpé chaque morceau, n'est lui pas équilatéral, mais isocèle et si on prend pour unité le coté du carré, la hauteur h1 qui est aussi la médiatrice de ce triangle équilatéral, est calculable c'est racine de 2 que divise 2 soit 0.707.
L'angle que font les faces inclinées par rapport à la face carré est calculable à partir de arctg de racine de 2 soit: 54° et 73/100
donc différents de 60° de plus de 5°.
Il faut incliner la lame de la scie de l'angle complémentaire à 90° soit: 35° et 27/100
Comme sur la photo suivante:
Réglage de l'inclinaison de la lame

On coupe alors selon la séquence suivante:
premier coté du tasseau, à gauche la chute, à droite le tasseau
deuxième coté du tasseau après retournement de la planche le tasseau est à gauche, mais cette méthode est très risquée pour nos phalanges et donc fortement déconseillée! Elle n'est ici que pour illustrer l'angle de coupe à ne faire qu'avec un berceau ou à la scie japonaise.
une fois que l'on a débité une longueur suffisante de tasseau isocèle on en coupe les extrémités avec le même angle en présentant le tasseau à la perpendiculaire.
ici le guide est à droite et la chute à gauche
Il ne reste qu'à faire la deuxième coupe par retournement pour obtenir exactement le carré au niveau du plan de la table de scie et les morceaux s'assemblent parfaitement.
Le guide est à gauche et la pièce finie à droite
On recommence pour avoir deux pièces identiques.
Arrondir légèrement les angles (sauf ceux des cotés de la face carréé) et les pointes au papier de verre pour des manipulations sans danger.
Rappel pour éviter les risques d'accident:
Bien entendu la protection de lame est retirée pour les besoins de la photo, la lame est arrêtée et exagérément sortie pour une visualisation plus pédagogique. Elle ne doit dépasser que d'un centimètre au plus.
Ne pas présenter des petites pièces dans une scie en rotation en les tenant entre les doigts. On peut les fixer sur un support type berceau qui glisse dans les rainures de la table avec des sauterelles de fixation et des cales coupées avec un angle complémentaire. les sauterelles servent aussi de poignées de manipulation en tenant les mains éloignées de la lame.
utilisez des martyres et des poussoirs pour éloigner vos doigts de la lame
Un peu dans ce genre;

Une solution encore plus sécuritaire fabriquer un berceau avec la scie sur table mais à partir de cales de grandes largeurs et couper à la scie japonaise sur des guides de coupes pour un état de surface sans rayures comme dans l'article sur le cluster.
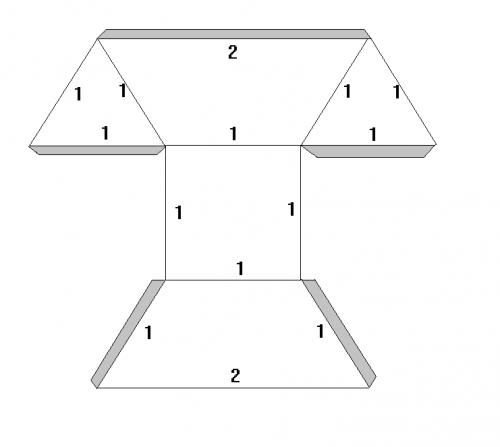
son développé pour bristol (approximatif il faut le dessiner avec précision):
Bien sur il en faut deux!
Le fichier en .stl pour le fabriquer avec une imprimante 3D
Les variantes sont innombrables quelques exemples:
tétraèdre en 4 morceaux
autre 4 morceaux
tétraèdre 5 morceaux
tétraèdre de cubes
tétraèdre de sphères
tétraèdre de dodécaèdre rhombiques
tétraèdre à pièces vissantes
tétraèdre enfermé dans un cube
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 196 autres membres