La trisection du carré de Bottcher une dissection géométrique élégante

On sait que certains problèmes ont des solutions avec des démonstrations géométriques qui n'utilisent que la règle et le compas.

Qu'il existe aussi des problèmes géométriques non solubles avec la règle et le compas comme la quadrature du cercle, la trisection d'un angle quelconque ou la duplication du volume du cube.

Une trisection du carré est constituée d'un jeu de pièces qui peuvent s'assembler soit en un grand carré soit en trois petits carrés dont la surface est par définition le tiers du grand carré.

On peut rechercher des trisections avec des propriétés remarquables comme avec le nombre de pièces le plus petit par exemple! Actuellement le record est de 6 pièces et il semble bien que ce soit le nombre minimum mais l'exactitude de cette affirmation n'est pas encore démontrée (un seul contre exemple démontrerai le contraire).

Il en existe plusieurs et bien que ce problème soit étudié depuis l'antiquité par des générations de mathématiciens la dernière découverte sur le sujet est assez récente et l'œuvre d'un amateur. C'est celle d'un copain Christian Blanvillain qui en 2010 a publié une solution totalement nouvelle avec seulement 6 pièces et justement une propriété particulière la surface de chaque pièce est égale!

Visitez son site qui donne les plus connues: http://www.qucub.com/home_fr

et bien d'autres renseignements comme l'histoire des recherches et découvertes sur le sujet.

Voici les neufs dissections les plus remarquables:

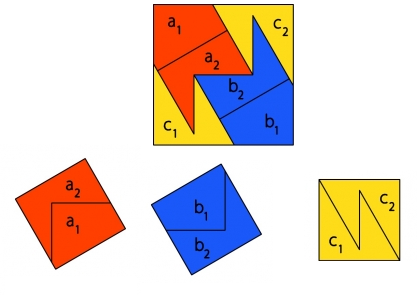
Lors de la réunion annuelle de la triche de 2015 (à laquelle je n'ai pas assistée à mon plus grand regret) Christian nous a fait un cadeau: la dissection de Bottcher en 10 pièces, ce qui ne constitue pas un record pour le nombre mais une curiosité car il s'agit de la seule dissection qui permet de faire 3 carrés de surface 1, un carré de surface 3 et un troisième problème avec un carré de surface 1 et un carré de surface 2.

L'ensemble des 10 pièces 2 fois les cinq mêmes.

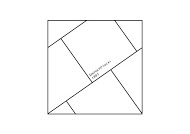
l'assemblage pour un seul de surface 3 (il n'y a qu'une solution):

un exemple pour les trois de un (il y a plusieurs solutions):

un exemple pour 1 + celui de 2 (il y a aussi plusieurs solutions):

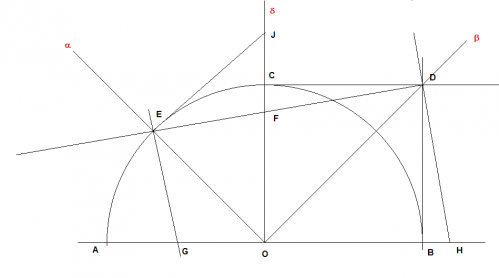
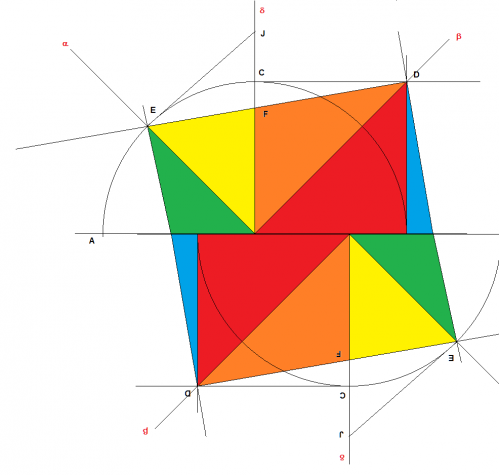
La construction géométrique avec la règle et le compas pour trouver les côtes exactes:

On part d'un demi-cercle de centre O et de diamètre AB=2 unités.

On trace perpendiculaire δ à AB passant par O et les bissectrices α et β des angles AOδ et BOδ

δ coupe le cercle en C

D est sommet du carré BOCD de coté unité donc sur β

α coupe le cercle en E

On trace la droite passant par ED elle croise δ en F

La perpendiculaire à ED en E coupe AO en G

La perpendiculaire à ED en D coupe AB en H

La perpendiculaire à EO en E coupe δ en J

Le triangle FCD est identique à HBD car:

CD=BD=1 et ils sont rectangles respectivement en C et B

CD est perpendiculaire à BD et FD à DH donc l'angle FDC= HDB

les angles encadrants les segments CD et BD sont respectivement égaux (CQFD).

Le triangle EGO est identique à EFJ car:

L'angle GOE fait 45° par construction et l'angle OJE a ses cotés OJ perpendiculaire à GO et EJ perpendiculaire à OE.

Le triangle OEJ est donc rectangle en E et isocèle EJO=EOJ=45° donc EO=1=EJ.

L'angle JEF et l'angle OEG car les cotés EJ perpendiculaire à EO et EF perpendiculaire à EG.

Un coté égal et deux angles égaux pour EGO et EFJ (CQFD)

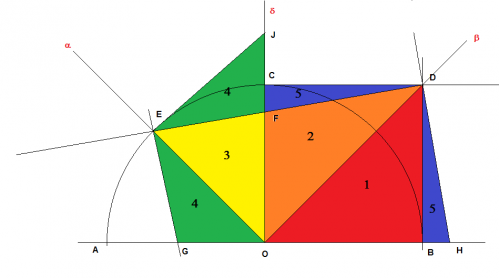
En conclusion on peut désigner les pièces comme suit par surface décroissante:

1= ODB = ODC (2+5) = OJE (3+4) sont des demi-carrés coupés par la diagonale

2= OFD

3= OFE

4= OEG = JEF

5= BDH = CDF

et OCD =2+5 est aussi un demi-carré comme OEJ=3+4.

Il est donc assez facile avec 6 demi-carrés de surface 1/2 de faire 3 carrés de 1 de surface ou 1 carré de 2 et 1 de 1 de surface. Par contre la démonstration de construction donne la solution de construction du carré de 3 qui elle est moins évidente.

Un très joli défi géométrique sera pour vous de (re)trouver une démonstration de construction des neuf cas de trisection du carré donnés dans le site de Christian Blanvillain.

Si comme d'habitude on me demande à quoi ça peut bien servir? Je réponds toujours: "au moins à faire plaisir à ceux qui aiment".

Il y a aussi la possibilité de fabriquer un jeu de trois tables carrées qui se transforment en une seule plus grande et toujours carrée, ou encore en une petite et une moyenne à partir d'un jeu de 6 à 10 pièces à trois pieds (quelques fois quatre).

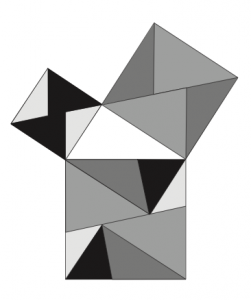
Johannes Eduard Böttcher (1847-1919) fut un physicien allemand. Il fut recteur du Realgymnasium de Leipzig, mais une grande partie de son travail d’investigation concernait les mathématiques pures. En 1886, il publia un modeste article dans la Revue pour l’enseignement des mathématiques et les sciences naturelles titré de manière très simple : « Modèle simple pour la démonstration du théorème de Pythagore ». Dans cet article, il proposa le casse-tête suivant :

Qui est aussi démontré par les figures suivantes:

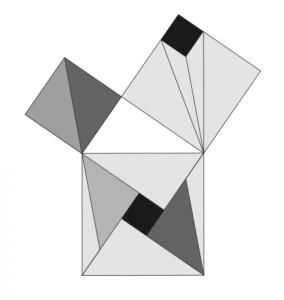
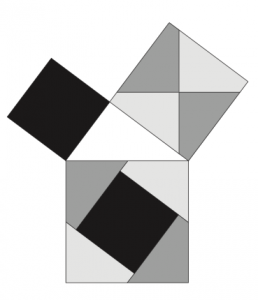
voir l’article

cet objet s'apparente aux dissections il en existe une quantité incroyable et certains auteurs les ont recensés dans des livres comme: