Puzzles & casse-tête en bois gratuits à fabriquer, construire soi-même

Le dé est un objet universel de nombreux jeux, ses propriétés sont connues:

il est cubique avec quelques fois les angles arrondis pour le faire rouler un peu plus facilement et donc, diminuer les risques de tricheries avec un lancer calculé.

Par convention généralement admise, le total de nombres de points sur chaque face est tel que la somme est constante pour deux faces opposées:

1+6 = 2+5 = 3+4 = 7.

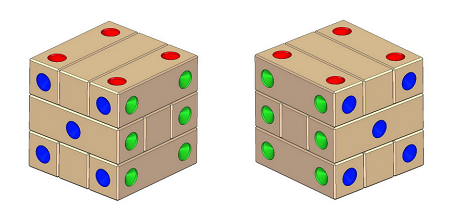
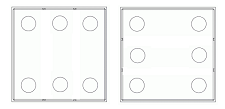
Peu de personnes savent qu'il existe deux sortes de dé, les dextrogyres et les lévogyres. Chacun est le résultat du reflet de l'autre dans un miroir comme une main gauche est le reflet de la main droite, mais cela n'a aucune influence sur les statistiques de tirages au sort. il faut remarquer que l'ordre des trois faces peuvent être positionnées comme ci-dessous sans aucune influence statistique pour un dé de jeu en un bloc unique.

Ensuite les positions pour les points des diagonales des faces à 2 et 3 points peuvent prendre chacune 2 possibilité, donc il existe 8 types de dés monoblocs différents.

figure 1

Ensuite, le dé peut devenir un casse-tête si on le divise en un certain nombre de pièces qui sont les dissections du cube.

Parmi les dissections du cube la plus courante est la dissection d'un cube en 3*3*3=27 cubes unitaires.

Une déclinaison encore plus simple est la dissection en groupe de 9 barres de 3 cubes unitaires de long qui vont s'assembler en trois couches croisées de trois barres comme l'image ci-dessus.

Si on y ajoute ensuite les combinaisons de points selon une des possibilités de dispositions pour les types de dé monoblocs on obtient un casse-tête très facile à construire! Mais il n'y en pas qu'un et le problème général est assez complexe à mettre en forme et surtout, à décrire car les conventions d'orientations successives dans l'espace demandent une méthode commune non évidente.

Le dénombrement se complique même avec cette dissection en 9 pièces que je viens de qualifier des plus simples!

J'en avais un depuis très longtemps et il m'avait paru trivial pour l'avoir résolu trop facilement. Mais un jour j'en ai manipulé un autre qui m'a causé une colle (comme d'habitude offert par Serge Piacentino que je remercie au passage). En cherchant la cause de mon échec, j'ai compris que ce casse-tête peut se présenter dans de nombreuses variantes du problème et des difficultés de niveaux qui sont eux aussi variables:

de simple et même d'évident, à plus complexe pour une forme identique, en fonction des différentes positions pour l'emplacement des points. 

En cherchant pourquoi et comment les recenser j'ai beaucoup hésité car ce problème se révèle lui aussi plus complexe qu'au premier abord, car la juxtaposition des contraintes n'additionne pas les solutions mais les multiplie avec des cas de simplification par symétries qui sont difficiles à reconnaitre et dénombrer et des cas triviaux qui sont moins intéressants à proposer.

figure 2

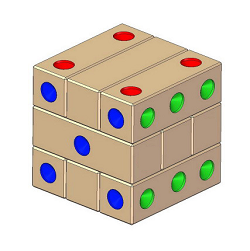
L'exemple ci-dessus montre un cas ou le repérage de l'emplacement des trois points alignés du 6 donnent une indication de départ particulière repérable qui facilite grandement la suite pour la recherche de la solution.

Ensuite bien que l'autre coté des trois faces visibles à 6, 5 et 4 points, il ne peut y avoir qu'une seule valeur:

le 1 en face du 6

le 2 en face du 5

le 3 en face du 4

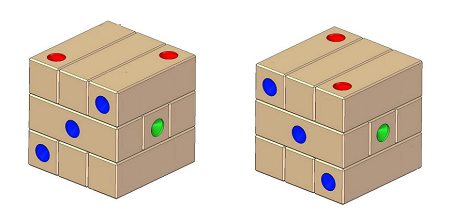
Si le 1 n'a qu'une possibilité de placement le 2 et le 3 peuvent chacun prendre deux possibilités sur des diagonales différentes d'une même face et indépendamment, ce qui pour notre famille de casse-tête multiplie les cas par 4.

figure 3

Décrire ces différentes positions dans l'espace à un lecteur, même avec des images, demande d'avoir une position de départ commune et un système de description des changements d'orientations successives selon trois axes, un peu comme les changements de rotations du Rubick's cube.

Pour être certain d'avoir étudié tout les cas on peut construire 96 cubes de 9 pièces avec toutes les possibilités d'y placer les points qui sont systématiquement creusés ou incrustés dans le bois et colorés et disposés sur:

6 faces possibles de départ pour y placer le 6

figure 4

Deux possibilités pour y disposer le 6 en vertical ou horizontal. On a vu que certaines combinaisons seront plus faciles à retrouver comme sur la figure 2...

figure 5

deux possibilités pour ensuite positionner le 5 et le 4 qui sont dextrogyre ou lévogyre (voir la figure 1 )

deux possibilités pour ensuite positionner le 2 face au 5 (voir la figure 3)

deux possibilités pour ensuite positionner le 3 face au 4 (voir la figure 3)

On a donc 6x2x2x2x2=96 cas de problèmes possibles

Pour différencier toutes les pièces de chaque groupe de 9 pièces sans risque de mélanges on peut :

teinter le bois de 8 façons différentes:

1 noir, 2 marron, 3 rouge, 4 orange, 5 jaune, 6 vert, 7 bleu, brut.

On peut aussi différencier les points de 7 façons différentes.

blanc, gris, violet, or, argent, bronze, et brut.

Il y a aussi des pièces qui n'ont pas de points pour ces pièces qui vont avoir la teinte générale du bois on peut y placer un point de taille réduite et de la couleur des points sur une face interne; donc cachée, de la pièce du cube assemblé pour rappeler le groupe de 9 pièces et les ranger sans mélange.

Fabrication pratique, repérage pour éviter les mélanges et relevé des solutions:

Du point de vue pratique j'utilise des carrelets de  20 mm que je débite en pièces de 60 mm de long par groupe de 9.

je les assemble en trois piles croisés (figure  4).

Ensuite je dessine les 6 points du six sur une des 6 faces possibles en choisissant une face de départ et si les 6 points seront verticaux ou horizontaux  (figure 5).

Je décide de faire un dextrogyre ou un lévogyre (figure 1).

puis les points du 3 en face du 4 et ceux du 2 en face du 5  (figure 3) en me choisissant également l'orientation de leurs diagonales.

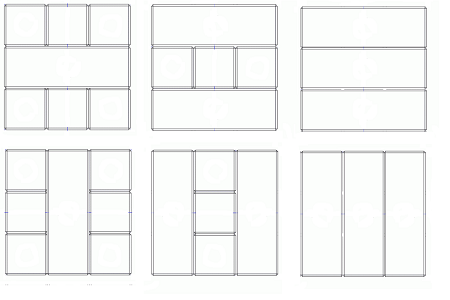
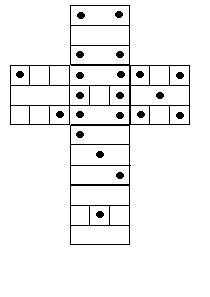
Pour repérer la solution de montage je reporte l'état du dé monté sur un éclaté en forme de croix et avec les orientations et les positions plus les couleurs choisies pour le bois et les points des pièces.

figure 6

Cette figure correspond à l'exemple donné dans le  .pdf du lien de  l’exemplaire donnée en début d'article qui utilise un repérage plus facile à utiliser mais moins facile à dessiner que sont ses pages 2 et 13 qui est dans l'image ci-dessous en bois brut et points noirs.

Sur les pièces bruts du dé une fois repérés les emplacements approximatifs des points, je dessine leur contour avec un gabarit pour obtenir un cercle de 8 mm de diamètre parfaitement centré, puis je creuse ensuite à la perceuse sur colonne avec une profondeur de 2 à 3mm.

Il n'y a plus qu'à teindre l'ensemble d'un groupe de 9 pièces puis l'intérieur des points en creux avec la couleur à chaque fois différente et reconstituer le dé avec le relevé de solution pour présenter le cube reconstitué.

D'ailleurs les solutions de dispositifs de présentation sont elles aussi un florilège d'astuces:

Tenu, soit par des élastiques, soit dans une boite dont 1 à 3 faces sont ouvertes ou sur un socle avec un couvercle transparent (là aussi les solutions sont multiples) et encore une double enveloppe croisée qui entoure 4 cotés; collée ou scotchée, etc...

Pour l'instant j'en ai fabriqué deux selon cette méthode.

j'avais demandé si l'un de mes lecteurs pouvait trouver une solution de représentation plus simple pour les recenser et les comparer tous, pour éventuellement exclure des groupes identiques capables de former plusieurs dés qui alors feraient doublons.

Sitôt dit Sitôt fait, un membre de l'air du bois, Jean-Christophe Filliatre a fait, dès le lendemain de la parution de l'article, un programme informatique et m'a fait parvenir la réponse!

En résumé on peut produire une grande famille de 96 casse-tête qui semblent identiques, mais qui sont différents en réalité et de difficultés très hétérogènes repérables pour éviter absolument les mélanges.

Mais on peut réduire l'ensemble à 56 groupes de 9 pièces soit 504 pièces repérées par la couleur du bois plus celles des points, pour lesquels les solutions sont notées sur une feuille qui propose pour chaque groupe un relevé qui comporte 1, 2 ou 4 possibilités de solutions selon la propriété du groupe.

Au passage un tour de magie avec un dé, avec le mode de construction qui va étonner à coup sur.

Une variante avec un  dé dont les pièces ne sont pas droite.