dissections du triangle équilatéral et autres
Suite à une vidéo proposée par youtube sur un casse-tête astucieux et original qui propose des dissections de polygones en triangle équilatéral:
Je me suis d'abord demandé si les dissections de cette vidéo sont exactes car on peut observer des vides ou plutôt des espaces avec un trop grand jeu entre certaines pièces dans plusieurs polygones.
Après quelques recherches sur le net j'ai constaté que les dissections sont toutes correctes pour les avoir retrouvées chacune, avec leur démonstration géométrique. Donc les jeux sont le résultat d'une découpe laser qui perd l'épaisseur du rayon.
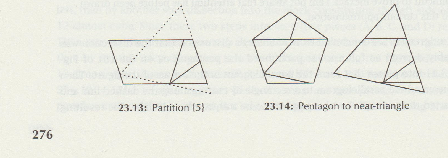
Tout d'abord, comme amélioration de départ possible avec le bouquin "dissections plane and fancy" de G.N. Fredrickson j'avais remarqué ça le pentagone 5 cotés en 5 pièces: sur son bouquin p 276
au lieu de 6 comme dans la vidéo
J'ai signalé ce fait à Gavin Theobald il m'a fait la réponse suivante:
"The dissection of triangle to pentagon from Greg Fredrickson’s book is not valid. The triangle is not equilateral. The dissection cannot be done in less than 6 pieces."
dont voici la traduction:
'La dissection du triangle en pentagone du livre de Greg Fredrickson n'est pas valide. Le triangle n'est pas équilatéral. La dissection ne peut se faire en moins de 6 morceaux."
Vérification faite Greg Fredrickson prend la précaution de dire dans son livre "near-triangle" ce qui sous-entend ou se traduit par presque le triangle (sous-entendu équilatéral).
Pour vous permettre de vérifier l'inexactitude de cette construction un lien sur les calculs et propriétés du triangle équilatéral
et un lien sur les calculs et propriétés du pentagone qui au passage donne les noms de tous polygones qui ont jusqu'à 100 cotés
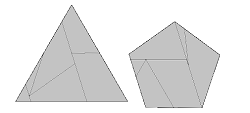
Donc, le pentagone 5 cotés en 6 pièces comme la vidéo: http://www.gavin-theobald.uk/HTML/Pentagon.html seule dissection exacte ou juste
hexagone 6 cotés en 5 pièces: https://demonstrations.
Heptagone 7 cotés en 8 pièces: https://demonstrations.
octogone 8 cotés en 7 pièces: https://www.youtube.com/watch?
enneagone 9 cotés en 8 pièces: sur bouquin p 145 plane and fancy de G.N. Frederickson
decagone 10 cotés en 7 pièces: http://www.gavin-theobald.uk/
Et pour améliorer avec des dissections correctes, on peut en ajouter 7 autres de plus:
le carré en triangle et donc réciproquement
le carré 4 cotés en 4 pièces: http://www.gavin-theobald.uk/
Le lien ci-dessus de ce site à partir du carré donne si on descend vers le bas toutes les déclinaisons jusqu'à 14 cotés et les 16 et 20, manque 15, 17 et 19 cotés, comme par hasard des nombres premiers.
hendecagone 11cotés en 11 pièces: http://www.gavin-theobald.uk/
dodecagone 12 cotés en 8 pièces: http://www.gavin-theobald.uk/
tridecagone 13 cotés en 12 pièces: http://www.gavin-theobald.uk/HTML/Triangle.html#Tridecagon
tetradecagone 14 cotés en 11 pièces: http://www.gavin-theobald.uk/HTML/Triangle.html#Tetradecagon
hexadecagone 16 cotés en 12 pièces: http://www.gavin-theobald.uk/HTML/Triangle.html#Hexadecagon
icosagone 20 cotés en 13 pièces: http://www.gavin-theobald.uk/HTML/Triangle.html#Icosagon
Les chercheurs ont donc encore du grain à moudre pour trouver les solutions des dissections du triangle équilatéral en polygones à 15, 17,18 et 19 cotés.
Tiens justement il y a des nombres premiers comme 17 et 19, je pense instinctivement que ces derniers sont plus résistant a solutionner...
La question que l'on doit se poser c'est:
Est-ce que chaque dissection est minimale pour le nombre de pièces?
La démonstration est certainement très difficile, par contre, un seul contre exemple suffit pour démontrer qu'une solution n'était pas minimale.
quelques liens en compléments sur les polygones et dissections:
Reste encore à le construire après avoir tracé chaque dissection de façon correcte géométriquement, ce qui n'est pas évident quand on sait déjà que certains polygones ne peuvent être tracés avec une règle et un compas.
Et de plus faire des découpes élément par élément comme en marqueterie à l'extérieur du trait (donc en laissant le trait à l'intérieur de chaque pièce) pour éviter les manques créés par l'épaisseur de la scie ou du rayon laser selon la technique de découpe dans le matériau brut.
Je n'ai pas encore trouvé le temps ni une technique pratique! Mais il y a bien un plus fou que moi qui va le réaliser pour nous le montrer.
Une autre idée présenter un set de même style avec les dissections du carré et les polygones réguliers, et pourquoi pas une présentation des dissections d'un polygone à d'autres.
On vient de démontrer que cette dissection est optimale:
On va améliorer l'article et ce casse-tête initial au fur et à mesure de mes trouvailles!
Retour aux articles de la catégorie casse-tête à construire ou connaître -
⨯
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 197 autres membres