Puzzles & casse-tête en bois gratuits à fabriquer, construire soi-même

 Facile à fabriquer par simple découpage à la scie vibrante à partir d'un carré mais toujours aussi fascinant, malgré son âge respectable de plus de 22 siècles.

Archimède de Syracuse, est né vers 287 av. J.-C. et mort dans la ville de Syracuse en 212 av. J.-C. C'est un mathématicien grec et non pas romain. Il les a bien au contraire combattu en protégeant sa ville Syracuse en Sicile de l'envahisseur romain avec des machines de guerre de son invention qui leur ont donné bien du fil à retordre!

Son lieu de naissance est Syracuse pour wikipédia et Samos pour une autre source!

Parmi ses inventions et découvertes on lui doit:

la vis sans fin

l'étude du levier avec sa phrase célèbre "donnez moi un point d'appui et je soulèverai le monde".

le roi Hiéron II de Syracuse (306-214) aurait demandé à Archimède (âgé alors de 22 ans seulement) de vérifier si une couronne d'or était totalement en or ou si l'artisan y avait mis de l'argent. C'est en réfléchissant dans un bain public qu'Archimède trouva la solution et poussa son non moins célèbre cri "Euréka!". Il venait de comprendre la poussée d'Archimède pour résoudre ce problème!

une méthode d’approximation de pi à l’aide de polygones réguliers et montre l'encadrement ${\displaystyle {\frac {223}{71}}<\pi <{\frac {22}{7}}}$.  De cette méthode, on a pu faire d’Archimède un précurseur du calcul infinitésimal....

et il est donc surprenant d'apprendre qu'il s'est penché sur un casse-tête géométrique. Ce qui démontre l'ancienneté de notre discipline, avec son stomachion; un découpage du carré 12*12...

Bien sur son découpage  présente des particularités géométriques particulières:

l’aire de chaque pièce est une fraction rationnelle de l’aire du carré (pour ceux qui ont oublié les cours du collège, un nombre entier divisé par un autre entier. Exemple: 24/144).

Il est composé de 14 pièces Design et copyright: Archimède … ( comme le dit Guy Brette)

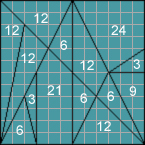2 pièces de 3 carreaux de surface

4 pièces de 6 carreaux de surface dont 2 identiques

1 pièce de 9 carreaux de surface

5 pièces de 12 carreaux de surface dont 2 identiques

1 pièce de 21 carreaux de surface

1 pièce de 24 carreaux de surface

Ce découpage est doté de possibilités innombrables d'assemblages entre les cotés de longueurs identiques ce qui permet aussi de nombreuses figures dans le style  du tangram (qui lui ne possède que 7 pièces)

Images extraites du site de Guy

Les réarranger pour les rentrer dans un carré de 12*12 semble difficile. Pourtant les solutions sont multiples mais rarement évidentes, ce qui en fait un casse-tête incontournable pour tout amateur du sujet. Les calculs sur les combinaisons mènent à 17 152 combinaisons possibles, dont 536, différentes à une isométrie près, permettant de reconstituer le carré.

 quelques liens sur le sujet:

  Les puzzles de la famille du Tangram par Philippe Moutou

http://www.mathpuzzle.com/MAA/04-Loculus%20of%20Archimedes/mathgames_11_17_03.html 

http://www.craftsmanspace.com/free-projects/stomachion-of-archimedes-puzzle-plan.html

Enregistrer