Les 3 cubes de Conway

Les 3 cubes de Conway problème

John Horton CONWAY est un mathématicien de l'université de Princeton et surtout l'inventeur du « jeu de la vie ».

Les trois découpages du cube sont d'une apparente simplicité et utilisent des pièces faciles à fabriquer (des cubes ou des parallélépipèdes réguliers).

Cette simplicité n'est qu'apparente puisque les solutions ne sont pas faciles à trouver par tâtonnements du fait que le petit nombre de forme de pièces limite certes le nombre de combinaisons mais pas la difficulté puisqu'en échange le nombre de placements possibles augmente ce qui agace rapidement.

Il faut pour résoudre ces problèmes baser son raisonnement sur les propriétés de parité et de symétrie.

Nombre et forme des pièces:

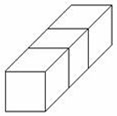
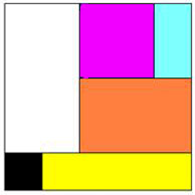
Cube 3x3x3

3 cubes unitaires

et 6 carrés 2x2

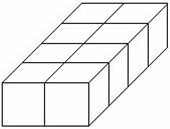
Cube 5x5x5 avec 5 cubes unitaires

5 cubes unitaires

6 fois

et 6 fois

2° Cube 5x5x5 avec 3 volumes 1x3

3 fois

13 fois

solutions

Il faut pour résoudre ces problèmes baser son raisonnement sur les propriétés de parité et de symétrie.

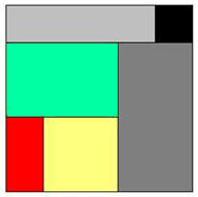
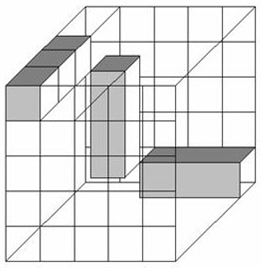
Pour le cube 3x3x3

Il est donc à cotés impairs les carrés de 2x2x1 sont pairs sur deux axes et impairs sur le troisième,il faut donc compléter au moins deux fois avec un cube 1x1x1 ou un 2x2x1 sur la tranche ça c'est pour la parité.

La symétrie nous indique que ce raisonnement doit jouer dans les trois dimensions et sur chaque colonne ou rangée.

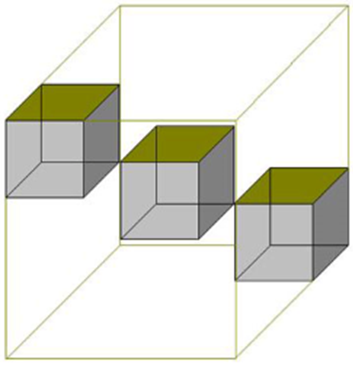
Comme nous n'avons que seulement trois cubes de 1 la logique nous indique que le meilleur placement de ces trois cubes de 1 se situe sur l'une des grandes diagonales du cube 3x3x3. Le reste est évident.

Le raisonnement est semblable pour les deux autres cubes 5x5x5 avec des variantes plus ou moins complexes (voir croquis)

Le principe