Le cristal japonnais
Le cristal japonais
(nom donné chez la marque Janod)
Autres noms (source le site de Chantal ):
STELLA chez LAGOON GAMES - Difficulté 4/5
MERCURE chez ARJEU - CT 1102 - Difficulté 2/6 - "Les Minis" - 7 cm
FUJIYAMA chez ARJEU - CT 30 - Difficulté 3/6 - 9 cm
IRMAN chez DALLOZ - Difficulté 2/5
CT 81 chez ARJEU - Difficulté 2/5

Ce casse-tête ne peut être solutionné par le logiciel Burrtools car il comporte une rotation de la clé.
Facile à fabriquer et relativement simple à monter et démonter (une fois que l'on connait l'astuce de la clé)
La vidéo du démontage sur dailymotion
La vidéo du montage sur youtube
La vidéo du remontage sur dailymotion
la vidéo du remontage sur youtube
Ou sous forme de dessin (source les casse-tête de Chantal):
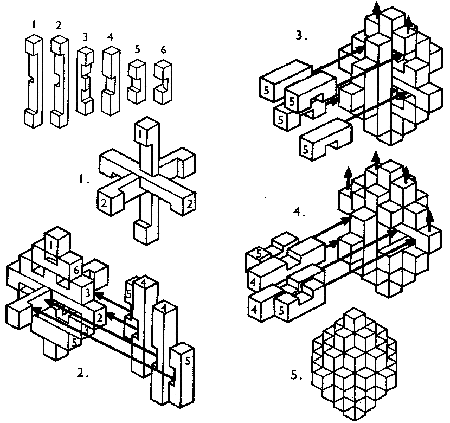
Sa fabrication
Nombre et forme des pièces:

En partant d'un carrelet d'une unité de coté (18 mm dans mon exemple)
Il y a:
10 morceaux de 3 unités de long dont 1 modifié pour faire la clé qui tourne
6 morceaux de 5 unités de long dont 2 modifiés
3 morceaux de 7 unités de long de deux types différents
soit 19 morceaux de 6 types différents
Chaque morceau est évidé sur la moitié de l'épaisseur au centre et sur une largeur d'1 unité pour les morceaux de 3 et 5 de longueur puis évidé sur un coté adjaçent d'une unité de largeur de chaque coté du centre pour deux morceaux de 5 de long et pour un de 3 de long (la clé) puis arrondi à la lime suivant ce profil (c'est ce qui permet à la clé de tourner):
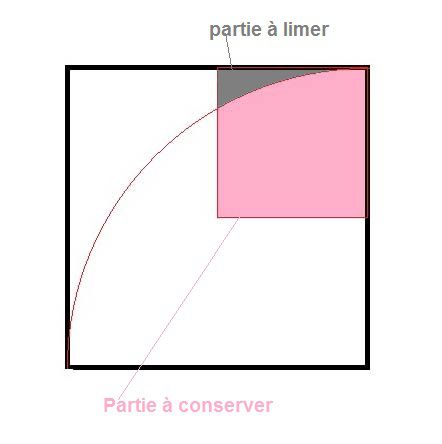
La partie à limer dépend du jeu entre les morceaux si ce jeu est important on n'aura pas besoin d'arrondir l'angle de la clé. Si ce jeu est nul il faudra retirer la totalité de la zone grisée. Entre les deux, on retirera une épaisseur proportionnelle au jeu dans le cas général.
Les morceaux de 7 de long sont évidés sur presque toute leur longueur sauf sur une unité de distance à partir des extrémités puis échancrés sur un coté adjacent d'une unité au centre pour les deux premiers et de la moitié d'unité accolée au centre mais décentré pour la dernière pièce.
Chacune de ces échancrures peuvent être faites sur une défonceuse sur table si l'on est équipé et entraîné à tenir et présenter d'aussi petites pièces dans un outil toujours dangereux pour un débutant (sans oublier un martyr en entrée et sortie pour éviter les éclats).
Sinon je recommande une méthode simple en utilisant une scie vibrante avec lame fine de type marqueterie qui permet d'effectuer chaque découpe sans risque, les quarts de tours dans les angles pouvant s'effectuer sans problème avec les lames fines de marqueterie.
Ou encore l'utilisation d'une scie à ruban avec un guide de profondeur plus sécuritaire.
La plus sécuritaire étant l'utilisation de scie japonaise avec guide orientable ou fabriqué avec des cales mais dans les deux cas il s'agit d'un matériel peu courant dans les ateliers européens.


Les traces de scie sont poncées ensuite pour obtenir un fini correct, sauf pour la scie japonaise qui évite cet inconvénient..
Il faut veiller à vérifier que chaque morceau permet l'emboitement à mi-bois exact et sans jeux. Ce qu'on vérifie en les croisant et en vérifiant qu'ils ne présentent aucun décalage d'épaisseur et un jeu minimum qui les maintient à angle droit .
Il en existe en fait toute une famille (photo extraite du site de Guy Brette):

3 5 7 9 11 13 15
Il vous sera facile de réaliser les plus petits de la famille. Une bonne dose d'imagination et de logique permettront de l'agrandir avec les plus gros, mais la quantité de bois et de découpes devient rapidement prohibitive.
La photo des éléments du premier avec 3 longueur de 3:

La photo de éléments du second avec longueur de 5:

La photo des éléments de celui de 9 de longueur:

je n'ai pas encore fabriqué les autres (les plus grands).
donc logiquement le nombre de pièces et leur forme se décomposent ainsi:
2 4 6 8 10
longueur mod mod mod mod mod total cubes pièces
3 3*3 9 3
5 3*5 6*3 24 9
7 3*7 6*5 10*3 81 19
9 3*9 6*7 10*5 14*3 161 33
11 3*11 6*9 10*7 14*5 18*3 281 51
13 3*13 6*11 10*9 14*7 18*5 22*3 449 73
15 3*15 6*13 10*11 14*9 18*7 22*5 26*3 673 99
etc...etc..
mod signifie modifié avec une échancrure supplémentaire de chaque coté du carré central et le chiffre précédent 2, 4, 6, 8, 10 etc... indique le nombre de ceux concernés dans le groupe de même longueur quand il est en rouge également.
Une autre façon de présenter beaucoup plus ordonnée celle d’Ishino
jusqu'à 13 de longueur et avec la formule générale.
Une vidéo du démontage du 11 marches
Une vidéo du montage du 11 marches
Une vidéo du montage du 15 marches
Une vidéo de la fabrication et montage du 17 marches
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 196 autres membres