La croix de Marseille ou du charpentier et la grande famille des burrs
Ce casse-tête quelques fois appelé croix de charpentier est un exemple célèbre et un représentant d'une famille bien plus large la famille des Burrs (les croix ou entrecroisés de Boer d’après le nom du mathématicien hollandais J.H De Boer).
Ils sont composés de 6 pièces et présentent la même forme extérieure une fois assemblés.
Visitez le site de rob où ils sont tous systématiquement recensés et résolus.
IBM avait aussi fait une étude systématique qui a disparu du net.
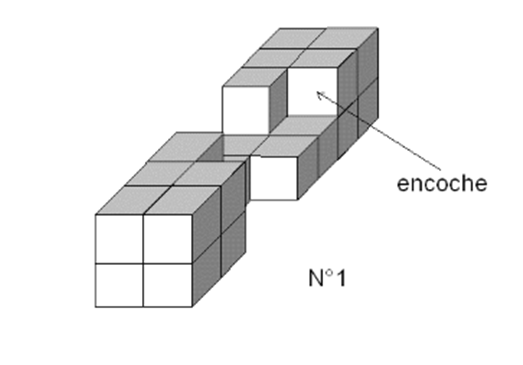
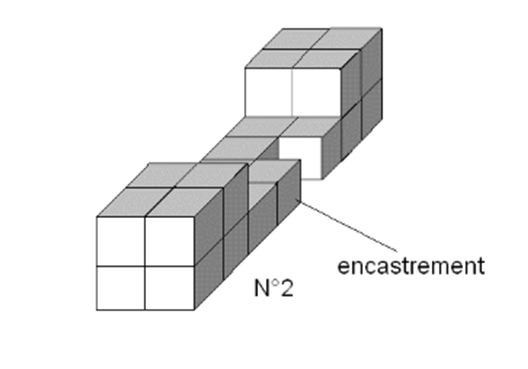
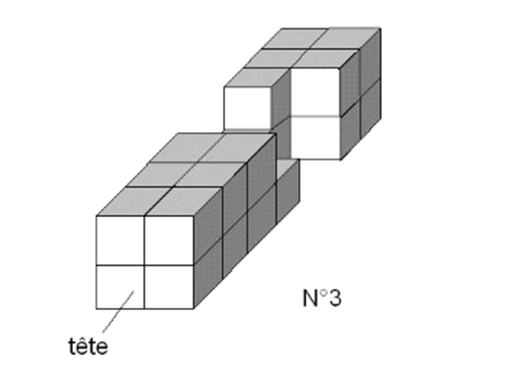
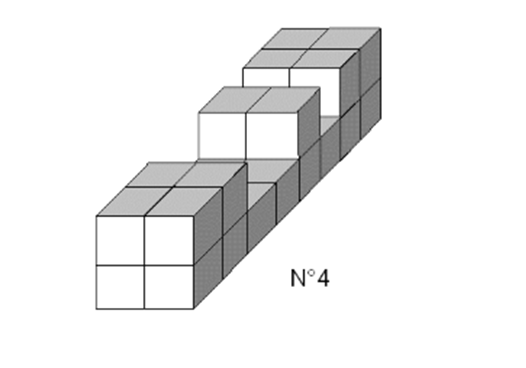
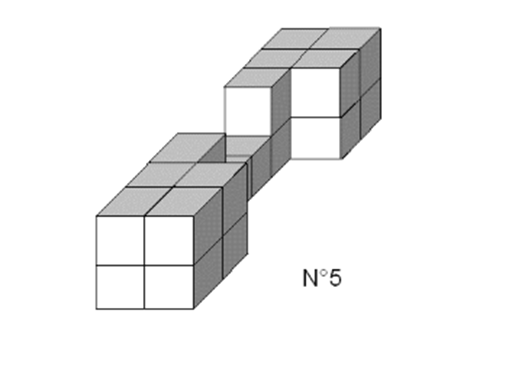
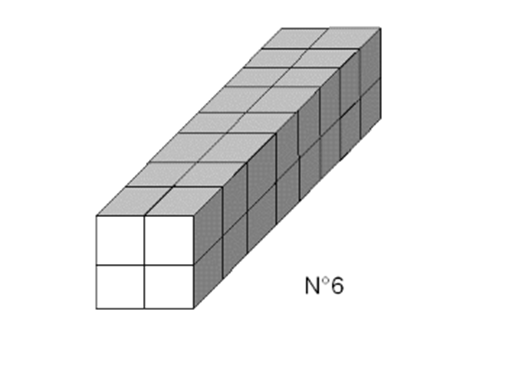
Forme des pièces N°1 à 6
ou encore avec une numérotation un peu différente:

Il faut remarquer que :
ordre de montage
•Tenir la pièce N°1 verticalement avec l'encoche tournée vers vous et vers le bas
• Positionner la pièce N° 2 horizontalement d'avant en arrière, orientée comme sur la figure « forme des pièces », avec l'encastrement dans l'encoche.
•
Positionner la pièce N°3, horizontalement orientée comme sur la figure « forme des pièces », dans l'axe de gauche à droite, avec la tête orientée vers votre droite.
•Positionner la pièce N°4 verticalement avec la fente d'un carreau de largeur vers le bas. Notez qu'il faut l'engager avec un « tiroir ».
Choix du bois: hêtre ou chêne (bois relativement dur) impérativement sec. Humidité résiduelle <10%.
Débit du bois: Dans un carrelet de 20mm de coté, couper six pièces de 80mmm de long. (donc dans 1m on pourra en débiter 2 en tenant compte des 3mm de trait de scie (80+3)*6=498mm presque 500)
outillage: scie sur table, fraiseuse sur table, fraise droite de 10mm de diamètre affûtée, berceau de maintient, cales de 10 et 20mm, ciseau à bois de 10mm.
20 pièces marquées de A à N avec des doublons pour certaines pièces.
Aucune marque, aucune info: je ne sais même pas à quoi doit ressembler le montage final. Cube, parallélépipède, lisse ou avec des aspérités!!!
Au dire du vendeur ( marché de Noël!!!! ) il faut chercher à fillo,, fylo, phylo, ou quelque chose comme çà!
Je pense qu'il a dit n'importe quoi.
Si quelqu'un peut me tuyauter un peu un grand merci d'avance!!
Je pense que çà doit bien bruler, mais avant je voudrais essayer quelque chose!! "
Son nom le "teufel set" soit l'assortiment du diable.
Il s'agit d'un set de burr dans le genre du célèbre " Bill Cutler set" qui lui, comporte 42 pièces 25 sortes et permet 314 combinaisons de croix.
Il faut assembler six pièces en croix de charpentier.
Le dernier problème c'est avec lesquelles?
voir:
http://robspuzzlepage.com/interlocking.htm
Il faut noter que la pièce pleine qui sert généralement de clé ne fait pas partie du lot.
Le livre 100 puzzles (how to make and solve them) d' Antony Filipiak page 86 montre un exemple avec un set de 38 pièces différentes dont 9 en double et 1 en triple soit 48 pièces au total qui permet la construction de 73 croix différentes et il nécessite la clé pleine dans 62 cas. Et en se limitant aux 62 cas il ne nécessite que 20 pièces différentes mais il faut 7 double et 1 triple ce qui fait 29 pièces. Malheureusement ce n'est pas celui qui nous préoccupe et il est nettement moins performant que le "Bil Cutler set".
Il faut signaler aussi le Set de Boer 29 pièces et 69 combinaisons qui est donné dans le livre 1000 casse-tête du monde entier p74 29 pièces, lui aussi moins performant que le set qui nous préoccupe et celui de Bill Cutler que l'on peut trouver dans le bouquin puzzles old and new p 68 et p154.
En cherchant un peu sur le net il y avait un lien avec "made by philos" justement:
http://www.cleverwood.com/teufel.htm mais ce lien est mort.
Mais ils disaient qu'il n'y a que 5 doubles et qu'il y aurait 159 croix possibles c'est intriguant!
Si je comprend bien l'historique au départ il n'y avait que 5 doubles plus la pièce pleine (notée O) et ça permet 151 croix puis en en la transformant en un double (lequel? en observant bien les photos il y a un double en B dont la couleur n'est pas identique c'est sûrement celui là qui remplace le O et en plus sur la page 2 du pdf il n'y a pas de cas avec 2*B) on a 159 croix possibles.
Il existait un lien pour le commander sur amazone Allemagne pour 18€ (délai 2 mois???)
Un exemple de collection en bois
Des logiciels de résolution à télécharger et surtout trouver du temps pour apprendre à s'en servir avec le tutorial:
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 196 autres membres