Flexaèdre et cube étoilé
La vidéo du Flexaèdre qui est une curiosité amusante à manipuler:
Composé de 12 tétraèdres non réguliers selon un patron assez simple et assemblés par des charnières:
Et avec quelques textures et coloriages on peut avec 4 flexaèdres former des figures encrore plus étonnantes:
une adresse pour en commander sur amazone.
ou sur amazone .fr.

Dans la même veine on déjà parlé du double cube étoilé: sur dailymotion
double cube étoilé sur youtube
Un assemblage qui m'a été montré par Jean-Jacques Dupas, un spécialiste des polyèdres
et le président de l’association Playmaths.
Une déclinaison les 3 cubes de Yoshimoto que l'on peut acheter tout fait et qui sont composés d'un flexaèdre d'un cube étoilé et d'un troisième cube séparé en 2 pour former un ensemble pour les manipuler comme dans cette vidéo
Les 3 cubes de Yoshimoto à fabriquer en carton avec les patrons dans la description de la vidéo
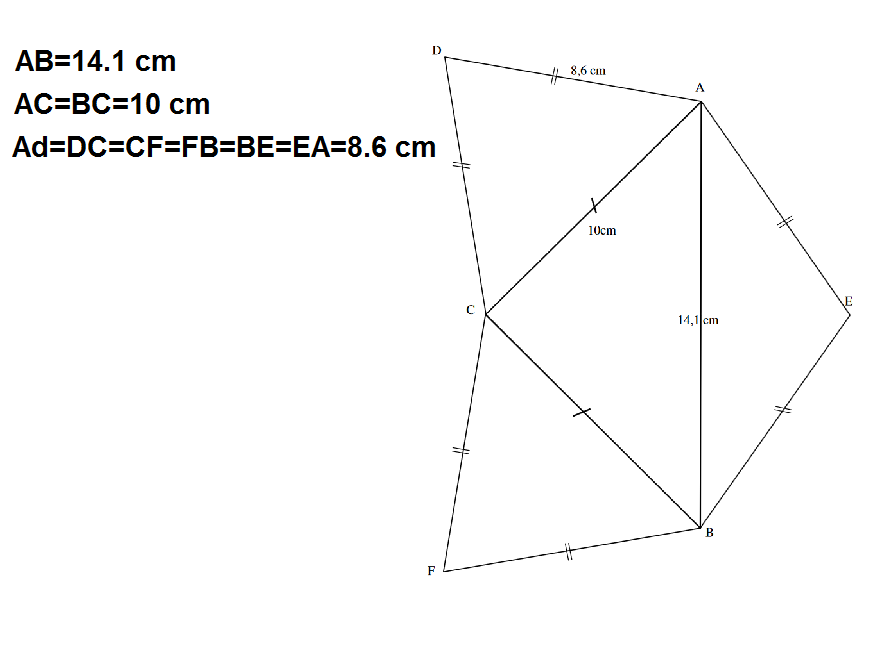
Chaque pseudo-cube du double cube est composé de 8 polyèdres eux-mêmes composés de 3 pyramides à base carrée et cotés en triangles équilatéraux.
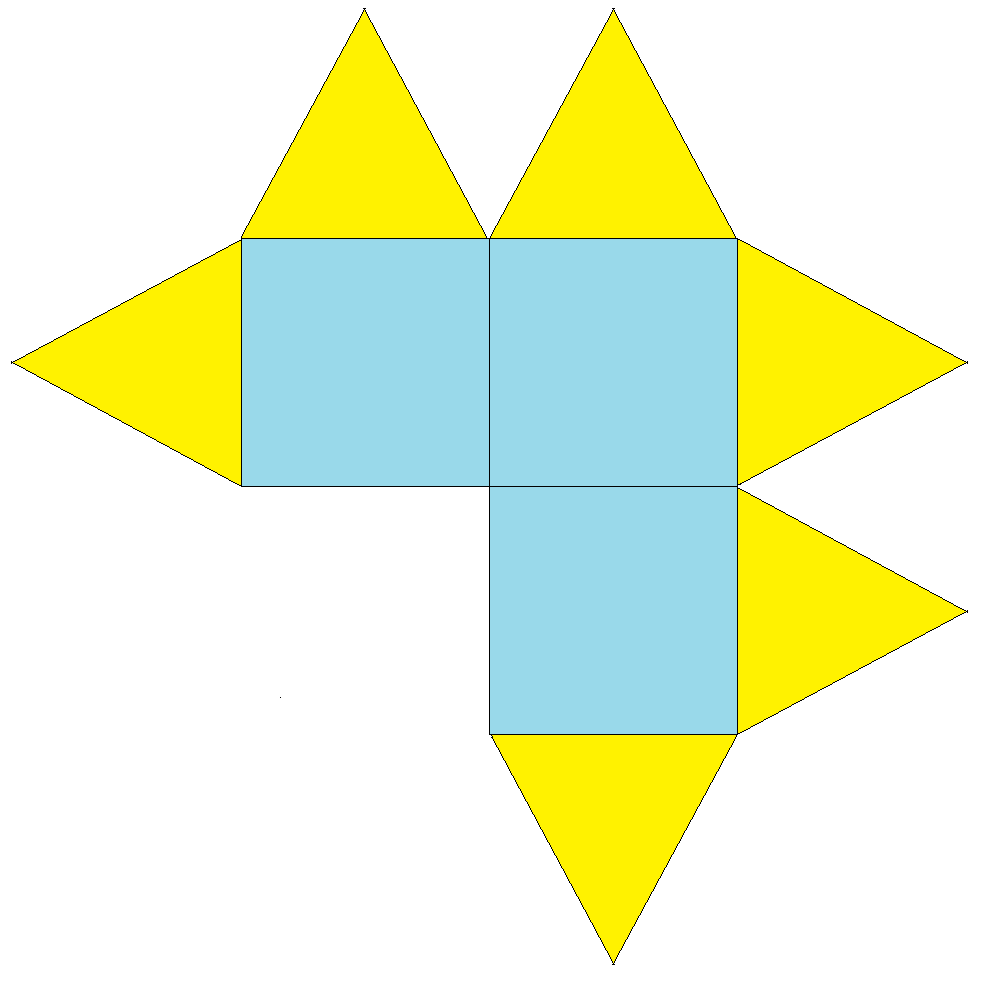
Le patron d'un des 8 polyèdres à assembler aussi par charnières. Il en faut donc 8 à carrés bleus et triangles jaunes et 8 à carré jaunes et triangles bleus:
Pour que les deux pseudo-cubes puissent réellement s'emboiter il est indispensable d'en avoir un dont le patron est un poil plus grand ou réciproquement un poil plus petit pour l'autre en fonction de l'épaisseur du carton utilisé pour la confection de l'ensemble. Le plus petit est fermé, le plus grand est ouvert.
Une autre vidéo pour une fabrication en origami.
Une vidéo pour le fabriquer en bois.
Un lien pour le fabriquer par imprimante 3D
Ces familles d'assemblages de dissections de polyèdres à charnières sont pour les volumes l'équivalent des dissections planes de polygones à charnières du livre" Hingeg Dissections: swinging & twisting" de Gerg N. FREDERICKSON. Mais la troisième dimension est bien plus difficile à "visualiser" et à exploiter pour trouver des dissections applicables aux polyèdres avec ou sans charnières.
Et il est possible de les combiner entre eux.
Un vaste domaine à explorer!
Par exemple je me demande si il existe un jeu de polyèdres qui pavent l'espace comme les dalles de Penrose pavent le plan, c'est à dire de façon non périodique, ou si cette question n'a pas de sens en trois dimensions?
il y a sur ce blog d'autres dissections:
la quadrature d’une portion de cercle.
Les dissections de lettres en carré
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 197 autres membres