Puzzles & casse-tête en bois gratuits à fabriquer, construire soi-même

 Trouver avec les seuls outils que sont la règle et le compas une transformation du cercle en carré est le graal de la géométrie.

A part cette exception qui s'apparente aux ambigrammes.

Aujourd'hui on sait que ce n'est pas possible car il faudrait trouver une construction du nombre Pi  or le nombre Pi est transcendantal ce qui signifie (en simplifiant) qu'il n'est pas exprimable avec une combinaison finie de nombres rationnels.

Il y a pourtant une  figure qui me pose un problème.

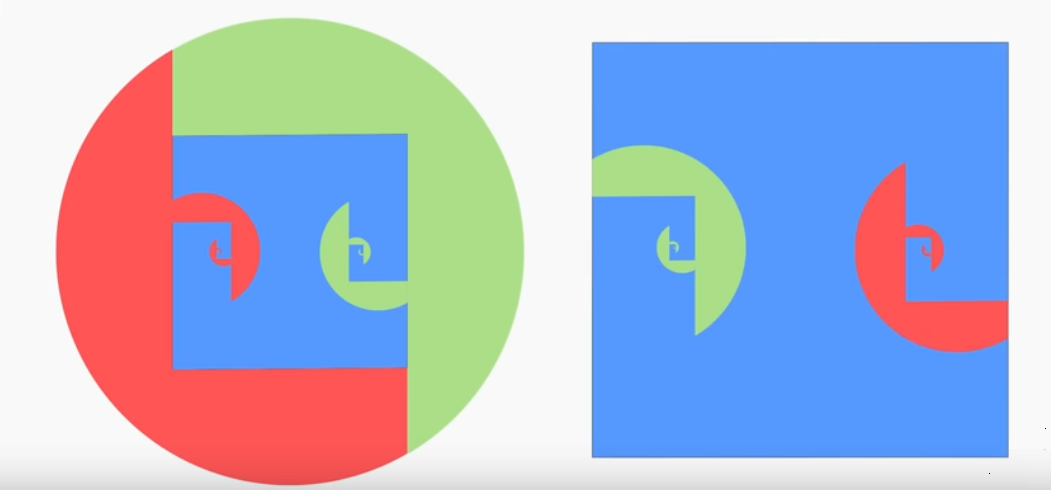
On conserve les formes par homothétie mais pas les dimensions.

On peut donc exprimer un développement de Pi avec des nombres réels sous forme de fractions si on sait calculer les surfaces de chaque pièces, étonnant non !

En fait on s'aperçoit vite qu'il faut les calculer avec une référence circulaire qui fait appel au nombre Pi.

Pourtant il semble possible d'approcher la quadrature du cercle avec les dissections de lunules ou croissants de cercle en figures parfaitement carrés ou en forme de croix grecques.

De telles transformations planes de fragments circulaires en carrés sont connues et continuent de troubler les cerveaux des mathématiciens (en herbe). C'est donc avec une pointe de jubilation que je vous propose les dissections suivantes extraites du livre les « inattendus mathématiques » de Jean-Paul Delahaye et particulièrement détaillées dans le livre de Greg Frederickson « Plane and Fancy ». Ces figures sont le résultat de recherches par les immenses spécialistes des dissections comme; Lindgren ou Dudeney après les travaux de Loyd's.

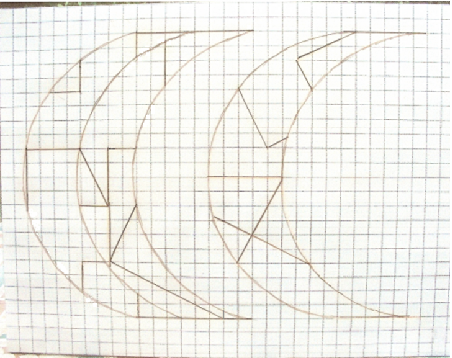
Tout d'abord il faut partir d'une grille de carrés (par exemple des carrés de 2*2 Cm ) puis à partir de ce fond fixer une feuille rigide de plastique transparent et tracer des arcs de cercles définis ainsi :

Leur rayon commun passe par la diagonale d'un rectangle de 2*10 carreaux (soit racine de 104 Cm).

Les centres des trois arcs de cercles sont alignés sur une même droite au milieu de deux parallèles qui sont séparées par 20 carreaux (donc 40 cm).

Les centres des ces arcs de cercles sur la ligne centrale sont séparés d'un intervalle de 4 carreaux.

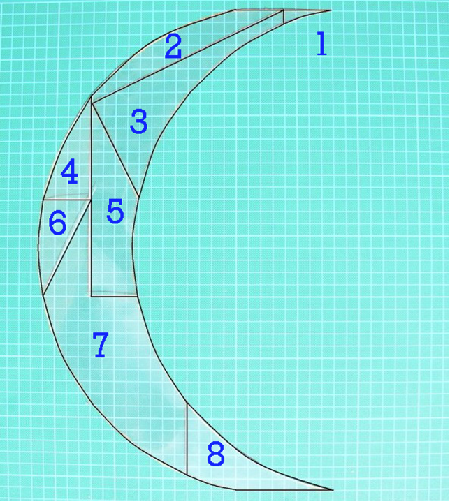
Après avoir tracé trois arcs de cercles successifs on obtient deux croissants de lune.

Après avoir découpé les croissants de lune et les morceaux selon le tracé, voici les assemblages sur un fond de tapis de coupe avec des carreaux d'un centimètre. Les déformations en tonneau sont dues aux défauts d'optique de l'appareil photo et les joints ont été soulignés en noir pour une meilleure lisibilité des photos.

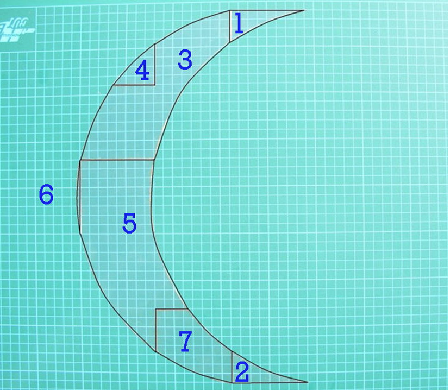
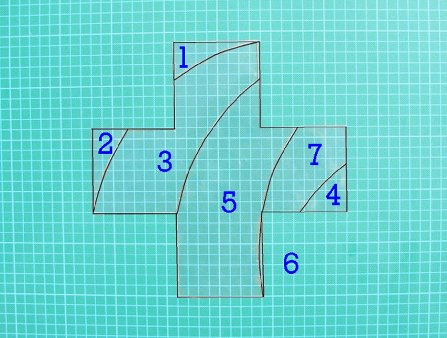
Pour le premier croissant de lune il existe une dissection en sept morceaux qui peut s'arranger en une croix grecque (la croix du pharmacien)

  (Nota il faut retourner la plus grande pièce 5)

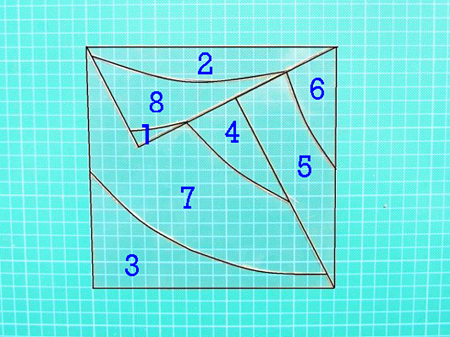
ou en huit morceaux pour le deuxième croissant pour arriver à un carré.

(Nota il faut retourner 3 pièces)

Une troisième transformation est obtenue avec un croissant constitué de deux demi-cercles de rayon 10 carreaux (donc 20cm et tangents aux deux droites parallèles) et dont les centres sont séparés de 5 carreaux sur la droite centrale. Leur dissection en 7 morceaux permet de construire une autre croix grecque.

 (Nota il faut retourner 3 pièces)

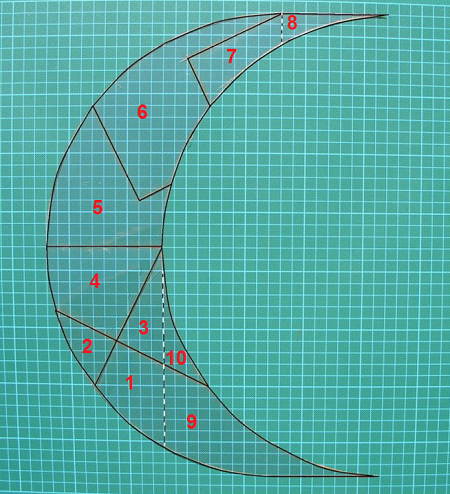
Il existe une dissection supplémentaire étonnante qui n'est pas dans le livre de Greg Frederickson à partir du même "patron" de lunule  en ajoutant deux coup de ciseaux supplémentaires selon les pointillés ce qui porte à dix le nombre de pièces, mais qui donne un carré au lieu d'une croix grecque comme ceci :

 La solution il faut retourner 4 pièces 5, 6, 7, 8:

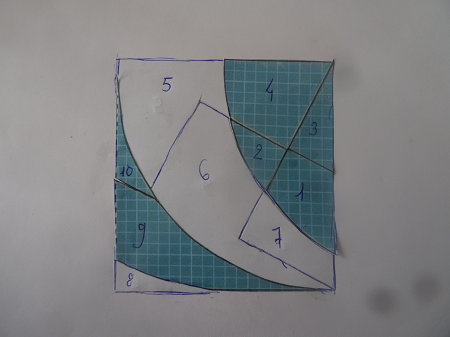
Le tracé n'est pas trop difficile mais les coupes sont délicates et un excellent exercice pour s'entraîner à la scie à chantourner le moindre défaut se traduit par un jour entre les pièces et il faut une grande régularité surtout dans les arcs de cercle qui doivent présenter un rayon particulièrement constant (ce qui peut être réalisé avec un axe fixe de rotation).

Pour les pièces réalisées sur les photos ci-dessus le meilleur résultat a été obtenu avec un support peu épais (film rhodoïd). Les contours sont tracés avec un compas à pointes sèches et marquage des parties rectilignes à la pointe à tracer puis coupe au cutter en suivant les sillons faits avec les pointes. On peut ensuite colorier à volonté.

Il reste une question (intéressante et difficile):

Ces dissections sont-elles minimales? C'est à dire construites avec le nombre minimal de morceaux.(sauf la dernière qui pour être minimale doit être réduite à 5 pièces en regroupant certains morceaux qui restent accolés). 

Un seul contre-exemple prouverai le contraire.

cet objet s'apparente aux dissections il en existe une quantité incroyable et certains auteurs les ont recensés dans des livres comme:

plane and fancy de Greg Frederickson ou Hinged Dissections: Swinging and Twisting

Ce dernier prenant en compte des contraintes supplémentaires comme les charnières ou le axes de retounement.

il y a d'autres dissections sur ce site:

la trisection du carré

Les dissections de lettres en carré 

les  dissections de volumes comme le fléxaèdre ou le cube étoilé

un exemple en bois.

petit supplément à propos de la quadrature du cercle:

La quadrature du cercle est simple mais pas avec la contrainte de n'utiliser qu'une règle et un compas!
1) avec une calculatrice:
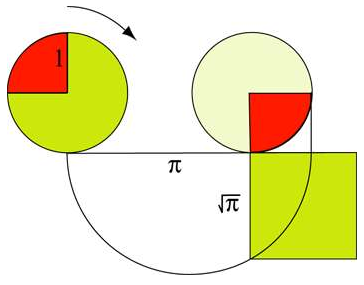
On sait que le carré doit avoir un coté égal à racine de pi multiplié par le rayon du cercle au carré
2) ou une construction géométrique astucieuse pour trouver le carré de même aire exemple:
https://static.blog4ever.com/2008/06/213622/quadrature-cercle.png

un cercle de rayon une unité roule sur une droite, après un demi-tour il parcours une longueur égale à sa demi-circonférence, soit pi au contact de la droite, la tangente au cercle coupe cette droite à une autre égale à pi+ 1. Le théorème de Pythagore permet alors de construire la longueur égale à la racine carrée de pi qui est le côté d'un carré de même aire que le cercle initial.
Cette construction est évidemment réversible et est la construction du cercle de même surface qu'un carré.
3) avec un découpage (ou dissection) c'est encore moins évident...
Miklós Laczkovich a résolut ce problème en 1989 : il a démontré qu'il était possible de découper un disque en un nombre fini de surfaces et de déplacer ces dernières pour qu'elles recouvrent exactement un carré. Il décompose le disque en 10 puissance 50 surfaces. La démonstration s'appuie sur l’axiome du choix, que la plupart des mathématiciens admettent aujourd'hui, mais qui n'est cependant qu'un axiome. La démonstration est très voisine dans l'esprit de celle du paradoxe de Banach-Tarski.
Assez peu accessible à tous.
Mais si Laczkovich a pu démontrer (en admettant l'axiome du choix) qu'un tel découpage existe, il ne l'a pas construit explicitement.

D'autres dissections de la croix.